信息熵 相对熵 交叉熵 KL散度 KL Divergence
信息熵
p(x):表示频率,即为概率
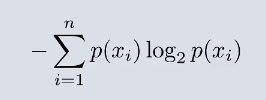
假设目前 有一个比赛 A的胜率为90%,B的胜率为10% 那么对于整场比赛来讲,
A的信息熵+B的信息熵 = 
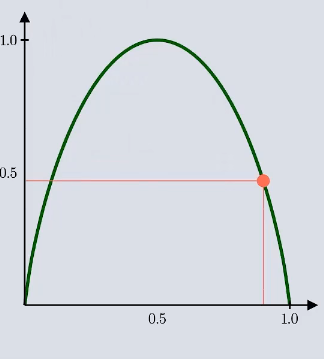
如果两者胜率都为50% 那么 其值为:
从这个两个例子可以看出对于越确定的事件 那么求出的值越小,越不确定的事件 求出的值越大.
假如把公式的自然底数改为e,10等其他底数可以发现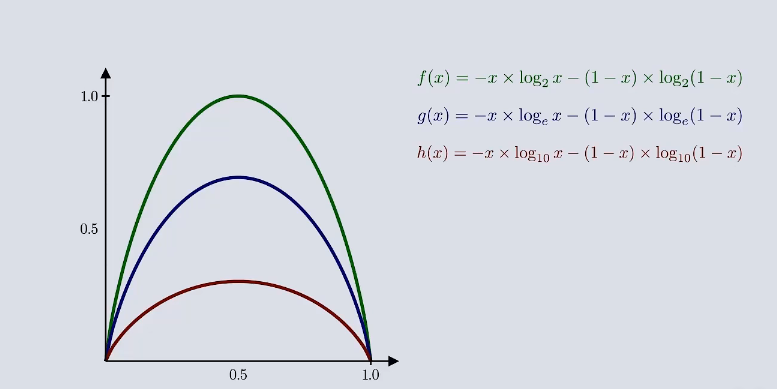
曲线的基本形状不发生改变 那么在机器学习中可以把底数省略 就可以得到信息熵的公式: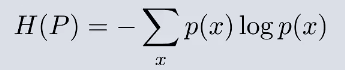
信息熵 ——>不确定性的度量
相对熵
大白话AI | 作弊也有学问? | 信息熵 | 相对熵 | 交叉熵 | KL散度 | KL Divergence_哔哩哔哩_bilibili
对于相对熵来讲,在确定了预测概率分布的情况下,对于实际概率分布 ,怎么可以获得冗余的大小呢?
预测概率函数*实际概率-实际概率的信息熵 = 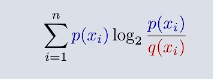
即为KL散度
对于该函数来说 函数值总是大于0的 那么这个函数可以用来衡量预测概率分布和真是概率分布的差异
对于两种概率分布来说,当两种概率分布越相似,其KL值越小,当两种概率分布差异越大,那么KL值越大
在机器学习中我们常常使用这种性质,通过最小化概率分布P和Q的相对熵,是两种概率分布逼近,神经网络通常需要
识别图片来分类,在神经网络中:
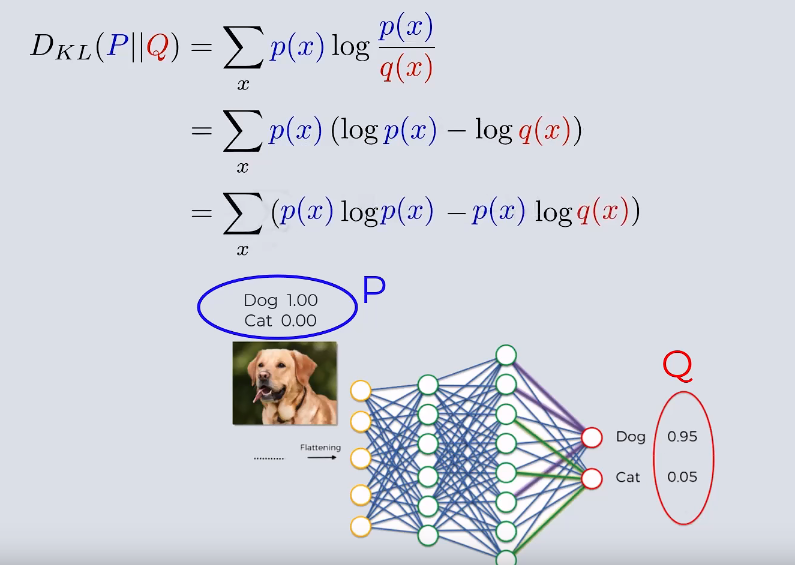
通过最小化相对熵 来实现 Q拟合样本 P的分布 来实现分类
所以在神经网络中 交叉熵损失函数就是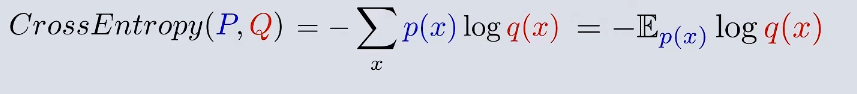
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.